THE NEWS
ABOUT THE CONFERENCE
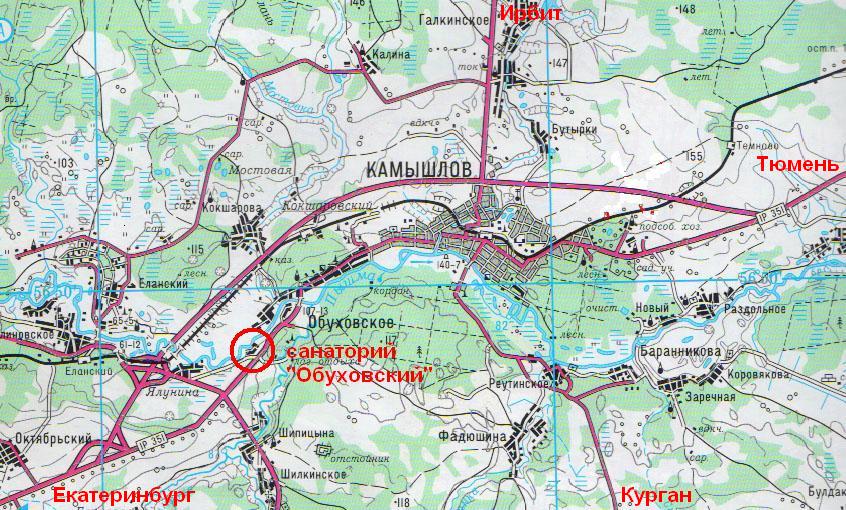
International conference “Mathematical Optimization Theory and Operations Research” (MOTOR2019) http://motor2019.uran.ru will be held on July 8-12, 2019, in a picturesque place near Ekaterinburg, Russia, at the borderline between Europe and Asia.
The conference brings together a wide research community in the fields of mathematical programming and global optimization, discrete optimization, complexity theory and combinatorial algorithms, optimal control and games, and their applications in relevant practical problems of operations research, mathematical economy, and data analysis.
Important dates
February 1, 2019
February 15, 2019
March 27, 2019
Call for papers:
Contact:
Previous events
MOTOR2019 is a descendant of a number of well-known International and All-Russian conferences, which were held in Ural, Siberia, and the Far East for a long time:
Conference name
Since
# in series
Last event
Baikal International Triennial School Seminar on Methods of Optimization and Their Applications, BITSS MOPT
1969
17
Discrete Optimization and Operations Research, DOOR
1996
9
MAIN TOPICS
- mathematical programming
- global optimization
- integer programming and combinatorial optimization
- computational complexity, approximation algorithms, schemes, bounds, heuristics and metaheuristics
- optimal control and game theory
- optimization and approximation
- optimization in machine learning and data analysis
- applications in operations research: scheduling, routing, facility location, packing and cutting, manufacturing systems, etc.
COMMITTEES
Program Committee Chairs
Program Committee
(to be extended)
Industry session chairs
Organizing Committee
INVITED SPEAKERS
Plenary lectures
Prof. Olga Battaia
ISAE-Supaero, Toulouse
France
Decision under ignorance: a comparison of existing criteria in a context of linear programming
Abstract: Decision or optimization problems often arise in an uncertain context. Depending on available information, several approaches have been proposed to model this uncertainty. In this talk, we focus on the case of low knowledge on possible states, namely decision under ignorance. In this case the decision-maker is able to give the set of possible values of optimization problem parameters but she/he is not able to differentiate them. We compare a set of criteria that can be used in this case on the example of a linear programming problem and discuss some possible applications.
Prof. Oleg Burdakov
Linkoping University
Sweden
Node partitioning and cycles creation problem
Abstract: We present a new class of network optimization problems, which extend the classical NP-hard travelling salesman problem. It is formulated as follows. Given a graph with a certain time associated with each node and each arc, a feasible partition of the nodes in subsets is such that, for each subset, there exists a Hamiltonian cycle whose travelling time is below the time associated with each node in the tour. It is required to find a feasible partitioning which minimizes the number of such cycles. Problems of this kind are typical in numerous applications, where services are repeatedly provided for a set of customers. For each customer, there is a critical time within which a service must be repeated. Given the travelling time between the customers, the set of customers is partitioned so that each subset is served by one agent in a cyclic manner without violating any individual critical time requirement. The number of agents is minimized. As an example, we consider a problem, in which a fleet of unmanned aerial vehicles is used for area patrolling. We introduce an mixed integer programming formulation of the node partitioning and cycles creation problem, and also heuristic algorithms for solving this problem. Results of numerical experiments are presented.
Joint work with: Kai Hoppmann, Thorsten Koch and Gioni Mexi (ZIB, Berlin, Germany)
Prof. Christoph Dürr
Sorbonne Université
France
Bijective analysis of online algorithms
Abstract: In the online computing framework the instance arrives in form a request sequence, every request must be served immediately, through a decision, which generates some cost. Think at the paging problem for memory caches. The goal in this research area is to identify the best strategy, also called online algorithm. Classically this is done through the competitive analysis, i.e. the performance of an online algorithm is compared with the optimal offline solution. The goal is to find an algorithm which minimizes this ratio over the worst case instance. You would say that algorithm A is better than algorithm B if it has a smaller ratio. However there are situations where two algorithms have the same ratio, still in practice one is better than the other. So people came up with a different technique to compare online algorithms directly with each other, rather than through the optimal offline solution. The bijective analysis is one of them. I would do a survey on this technique, and talk about a related personal work: Best-of-two-worlds analysis of online search, with Spyros Angelopoulos and Shendan Jin.
Prof. Alexander Grigoriev
Maastricht University
Netherlands
A survey on possible and impossible attempts to solve the treewidth problem via ILPs
Abstract: We survey a number of integer programming formulations for the pathwidth and for the treewidth problems. The attempts to find good formulations for the problems span the period of 15 years, yet without any true success. Nevertheless, some formulations provide potentially useful frameworks for attacking these notorious problems. Some others are just curious and interesting fruits of mathematical imagination.
Prof. Mikhail Kovalyov
United Institute of Informatics Problems NASB
Belarus
No-idle scheduling of unit-time jobs with release dates and deadlines on parallel machines
Abstract: While the problem of scheduling unit-time jobs with release dates and deadlines on parallel machines is polynomially solvable via a reduction to the assignment problem, the no-idle requirement destroys this reduction and makes the problem challenging. In the presentation, a number of properties of this problem are reported, and heuristic and optimal algorithms based on these properties are described.
Prof. Vadim Levit
Ariel University
Israel
Critical and Maximum Independent Sets Revisited
Abstract: A set of vertices of a graph is independent if no two its vertices are adjacent. A set is critical if the difference between its size and the size of its neighborhood is maximum. Critical independent sets define an important area of research due to their close relationships with the well-known NP-hard problem of finding a maximum independent set. Actually, every critical independent set is contained in a maximum independent set, while a maximum critical independent set can be found in polynomial time. If S is an independent set such that there is a matching from its neighborhood into S, then it is a crown. It is known that every critical independent set forms a crown. A graph is König-Egerváry if every maximum independent set is a crown. Crowns are also accepted as important tools for fixed parameter tractable problems. For instance, the size of the vertex cover can be substantially reduced by deleting both the vertices of a crown and its neighborhood. In this presentation, we discuss various connections between unions and intersections of maximum (critical) independent sets of graphs, which lead to deeper understanding of crown structures, in general, and König-Egerváry graphs, in particular.
Prof. Bertrand M.T. Lin
National Chiao Tung University, Hsinchu
Taiwan
An Overview of the Relocation Problem
Abstract: The relocation problem is formulated from a municipal redevelopment project in east Boston. In its abstract form, the relocation problem incorporates a generalized resource constraint in which the amount of the resource returned by a completed activity is not necessarily the same as that the activity has acquired for commencing the processing. We will first introduce the connection of the relocation problem to flow shop scheduling. Several traditional scheduling models with the generalized resource constraints have been proposed investigated. We will review existing results, suggest new models and present several open questions.
Prof. Natalia Shakhlevich
University of Leeds
United Kingdom
On a New Approach for Optimization under Uncertainty
Abstract: Research on decision making under uncertainty has a long history of study. Still theoretical findings have strong limitations: stochastic programming requires probability distributions for uncertain parameters which are often hard to specify; robust optimisation essentially relies on worst-case scenarios which can be over-pessimistic and far from realistic scenarios; stability analysis explores optimal solutions which can be hard to find even for well predicted scenarios. As an alternative approach, we propose a new system model based on the concept of resiliency. Resilient solutions are not required to be optimal, but they should keep quality guarantees for the widest range of uncertain problem parameters. The talk illustrates key steps of resiliency analysis considering examples of 0/1 combinatorial optimisation problems.
Prof. Angelo Sifaleras
University of Macedonia
Greece
Exterior Point Simplex-type Algorithms for Linear and Network Optimization Problems
Abstract: Two decades of research led to the development of a number of efficient algorithms that can be classified as exterior point simplex-type. This type of algorithms can cross over the infeasible region of the primal (dual) problem and find an optimal solution reducing the number of iterations needed. Thus, such approaches aim to find an efficient way to get to an optimal basis via a series of infeasible ones. In this lecture, we present the developments in exterior point simplex-type algorithms for linear and network optimization problems, over the recent years. We also present other approaches that, in a similar way, do not preserve primal or dual feasibility at each iteration such as the monotonic build-up Simplex algorithms and the criss-cross methods, and also discuss some open research problems.
Prof. Vitaly Strusevich
University of Greenwich
United Kingdom
Design of Fully Polynomial Time Approximation Schemes for Non-linear Boolean Programming Problems
Abstract: The talk is aimed at describing various techniques used for designing fully-polynomial approximation schemes (FPTAS) for problems of minimizing and maximizing non-linear non-separable functions of Boolean variables, either with no additional constraints or with linear knapsack constraints. Most of the reported results are on optimizing a special quadratic function known as the half-product, which has numerous scheduling applications. Besides, problems with a more general objective and nested linear constraints are considered and a design of an FPTAS based on the K-approximation calculus is discussed.
Tutorials
Prof. Tatjana Davidović
Mathematical Institute of the Serbian Academy of Sciences and Arts
Serbia
Distributed memory based parallelization of metaheuristic methods
Abstract: Metaheuristics represent powerful tools for addressing hard combinatorial optimization problems. However, real life instances usually cannot be treated efficiently by the means of computing times. Moreover, a major issue in metaheuristic design and calibration is to provide high performance solutions for a variety of problems. Parallel metaheuristics aim to address both issues. The main goal of parallelization is to speed up the computations by dividing the total amount of work between several processors. Parallelization of stochastic algorithms, such as metaheuristics may involve several additional goals. Besides speeding up the search (i.e., reducing the search time), it could be possible to: improve the quality of the obtained solutions (by enabling searching through different parts of the solution space); improve the robustness of the search (in terms of solving different optimization problems and different instances of a given problem in an effective manner; robustness may also be measured in terms of the sensitivity of the metaheuristic to its parameters); and solve large-scale problems (i.e., solve very large instances that cannot be even stored in the memory of a sequential machine). A combination of gains may also be obtained: parallel execution can enable an efficient search through different regions of the solution space, yielding an improvement of the quality of the final solution within a smaller amount of execution time. The objective of this talk is to present a state-of-the-art survey of the main ideas and strategies related to the parallelization of metaheuristic methods. Various paradigms related to the development of parallel metaheuristics are explained. Among them, communications, synchronization, and control aspects are identified as the most relevant. Implementation issues are also discussed, pointing out the characteristics of shared and distributed memory multiprocessors as target architectures. All these topics are illustrated by the examples from recent literature related to the parallelization of various meta-heuristic methods, with the focus on distributed memory parallelization of Variable Neighborhood Search (VNS) and Bee Colony Optimization (BCO) using Message Passing Interface (MPI) communication protocol.
Prof. Stephan Dempe
TU Bergakademie Freiberg
Germany
Bilevel optimization: The Model and its Transformations
Abstract:
Bilevel (or hierarchical) optimization problems aim to minimize one function subject to (a subset of) the graph of the solution set mapping of a second, parameter dependent optimization problem. The parameter is the decision variable of the socalled leader, the optimization problem describing the constraints is the problem of the follower. These problems have a large number of applications in science, engineering, economics. To investigate and solve them, they need to be transformed into a single-level optimization problem. For that different approaches can be used.
1) If the follower’s problem is regular and convex, it can be replaced using the Karush-Kuhn-Tucker conditions. The result is a so-called Mathematical Program with Equilibrium Constraints. In these nonconvex optimization problems, the Mangasarian-Fromovitz constraint qualification is violated at every feasible point. Solution algorithms converge (under suitable assumptions) to stationary points which are, in general, not related to stationary points of the bilevel optimization problem. To overcome this unpleasant situation, a certain regularization approach can be used. Another approach uses the transformation to a mixed integer (nonlinear) optimization problem.
2) If the optimal value function of the follower’s problem is used, a nonconvex, nonsmooth optimization problem arises. Again, the (now nonsmooth) Mangasarian-Fromovitz constraint qualification is violated at every feasible point. If the optimal value function is convex or concave, its approximation is helpful to describe a solution algorithm. Optimality conditions can be derived using partial calmness or a certain penalization approach.
3) The problem can be reformulated as a generalized Nash equilibrium problem.
Topic of the lecture is the introduction of the model together with some surprising properties and a short overview over promising accesses to investigate and solve it.
Prof. Oleg Khamisov
Melentiev Energy Systems Institute SB RAS
Russia
The fundamental role of concave programming in continuous global optimization
Abstract: A comprehansive description of connections between concave programming and other branches of global optimization like Lipschitz optimization, d.c. optimization etc. is given. It is shown that in general solution of almost every global optimization problem can reduced to solution of a sequence of concave programming problems. Modern concave optimization technology including cuts, branch and bounds, branch and cuts and so on as well as the corresponding extensions to different global optimization problems are presented. A part of the talk is devoted to the connection between concave and mixed 0-1 linear programming.
Prof. Alexander Kononov
Sobolev Institute of Mathematics
Russia
Primal-dual Method and Online Problems
Abstract: The primal-dual method is a powerful tool in the design of approximate algorithms for combinatorial optimization problems. In our tutorial we discuss how this method can be extended to develop online algorithms. The tutorial is based on the survey by N. Buchbinder and J. Naor and the web-presentation by N. Bansal.
Prof. Nenad Mladenovic
Emirates College of Technologies
Abu Dhabi, UAE
Solving nonlinear system of equations as an optimization problem
Abstract: The Nonlinear System of Equations (NSE) problem is usually transformed into an equivalent optimization problem, with an objective function that allows us to find all the zeros. Instead of the usual sum-of-squares objective function, the new objective function is presented as the sum of absolute values. Theoretical investigation confirms that the new objective function provides more accurate solutions regardless of the optimization method used. In addition, we achieve increased precision at the expense of reduced smoothness. In this paper, we propose the continuous variable neighbor-hood search method for finding all the solutions to a NSEs. Computational analysis of standard test instances shows that the proposed method is more precise and much faster than two recently developed methods. Similar conclusions are drawn by comparing the proposed method with many other methods in the literature.
Joint work with: Jun Pei, Zorica Drazic, Milan Drazic, Panos M. Pardalos
Prof. Evgeni A. Nurminski
Far Eastern Federal University
Russia
Projection Problems and Problems with Projection
Abstract: This lecture reviews the state of the art for probably the most common computational operation in applied mathematics --- projection, which can be also considered as the problem of finding the least norm element (LNE) in a given subset of a linear vector space. The special attention in the lecture will be given to Euclidean or orthogonal projection, but we plan to discuss another norms as well. Projection is computationally intensive operation even for relatively simple sets like canonical simplexes and special algorithms are a way more efficient than off-the-shelf quadratic programming methods especially for large-scale problems. Large-scale projection problems can be decomposed in different sequential or parallel manner as extension of celebrated Kaczmarz sequential projection procedure and block-row action methods. We discuss also the problem of numerical instability of projection operation which is quite common in such applications as new optimization algorithms, linear programming, machine learning and automatic classification.
Prof. Alexander Strekalovsky
Matrosov Institute for System Dynamics and Control Theory SB RAS
Russia
Modern methods of nonconvex optimization
Abstract: We address the nonconvex optimization problem with the cost function and equality and inequality constraints given by d.c. functions. The linear space of d.c. functions possesses a number of very attractive properties. For example, every continuous function can be approximated at any desirable accuracy by a d.c. function and any twice differentiable function belongs to the DC space. In addition, any lower semicontinuous (l.s.c.) function can be approximated at any precision by a sequence of continuous functions. Furthermore, provided that for the optimization problem under study we proposed the new Global Optimality Conditions (GOCs), which have been published in the English and Russian languages. The natural question arises: is it possible to construct a computational scheme based on the GOCs (otherwise, what are they for?) that would allow us not only to generate critical points (like the KKT-vectors) but to escape any local pitfall, which makes it possible to reach a global solution to the problem in question? First of all, we recall that with the help of the Theory of Exact Penalization, the original d.c. problem was reduced to a problem without constraints. Moreover, it can be readily seen that this penalized problem is a d.c. problem as well. Furthermore, special Local Search Methods (LSMs) were developed and substantiated in view of their convergence features. In addition, the GOCs were generalized for the minimizing sequences in the penalized problem. A special theoretical method was proposed and its convergence properties were studied. We developed a Global Search Scheme (GSS) based on all theoretical results presented above, and, moreover, we were lucky to prove that the sequence produced by the GSS turned out to be minimizing in the original d.c. optimization problem. Finally, we developed a Global Search Method (GSM), combining the special LSM and the GSS proposed. The convergence of the GSM is also investigated under some natural assumptions. The first results of numerical testing of the approach will be demonstrated.
PAPER SUBMISSION
Authors are invited to submit their papers reporting on novel results that are not published or submitted simultaneously to any journal or another conference with refereed proceedings. Papers should be prepared in the Springer LNCS Format, can have 12-15 pages, and submitted in PDF. Please, follow the official Springer authors guidelines and LNCS Latex templates. All papers should be submitted through the easychair conference management system, which is available now.
Abstracts
Proceedings
Conference proceedings will be published by Springer Nature as volumes of Lecture Notes in Computer Science (LNCS) and Communications in Computer and Information Science (CCIS) series.
Lecture Notes in Computer Science
Accepted papers
Corresponding authors of the listed papers are invited to upload camera-ready versions of their papers through Easychair until April 7, 2019.
Please, login as a proceedings author and upload the files according to the instructions as follows:
- a zipped file containing all latex sources, images, and answers to the reviewers' comments; please, name this file paper-NNN.zip, where NNN is the number of your paper
- PDF version of your camera-ready paper
- scan-copy of the Copyright form, filled and signed by the corresponding author. The prefilled form you can download here.
Please note that at least one author should participate in the conference and pay the registration fee in order to have your paper included in the proceedings.
Communications in Computer and Information Science
Accepted papers
Corresponding authors of the listed papers are invited to upload camera-ready versions of their papers through Easychair until June 30, 2019.
Please, login as a proceedings author and upload the files according to the instructions as follows:
- a zipped file containing all latex sources, images, and answers to the reviewers' comments; please, name this file paper-NNN.zip, where NNN is the number of your paper
- PDF version of your camera-ready paper
- scan-copy of the Copyright form, filled and signed by the corresponding author. The prefilled form you can download here.
Please note that at least one author should participate in the conference and pay the registration fee in order to have your paper included in the proceedings.
Special issues
Papers significantly extending the results presented at the conference MOTOR 2019, or related papers, will be considered for peer-reviewed publication in special issues of the following journals:
Journal of Global Optimization
Optimization Methods & Software (OMS)
Yugoslav Journal of Operations Research
Discrete Analysis and Operations Research
Submission dates and instructions
January 10, 2020
REGISTRATION FEES
- Last name:
- Given name(s):
- Affiliation(s), including address(es):
- Citizenship:
- Are you a student (PhD student) (yes - please, enclose a scan-copy of your student ID card / no):
- ID(s) and title(s) of your papers(s), including all authors:
- Preferred way of payment (wire transfer (RUB / EUR), bank card online, cash (on site)):
- Do you need visa support (yes / no):
- Preferred type of entry visa (Business / Tourist):
- Do you need an invitation letter for your employer (electronic, hard copy, both, none):
- Any comments:
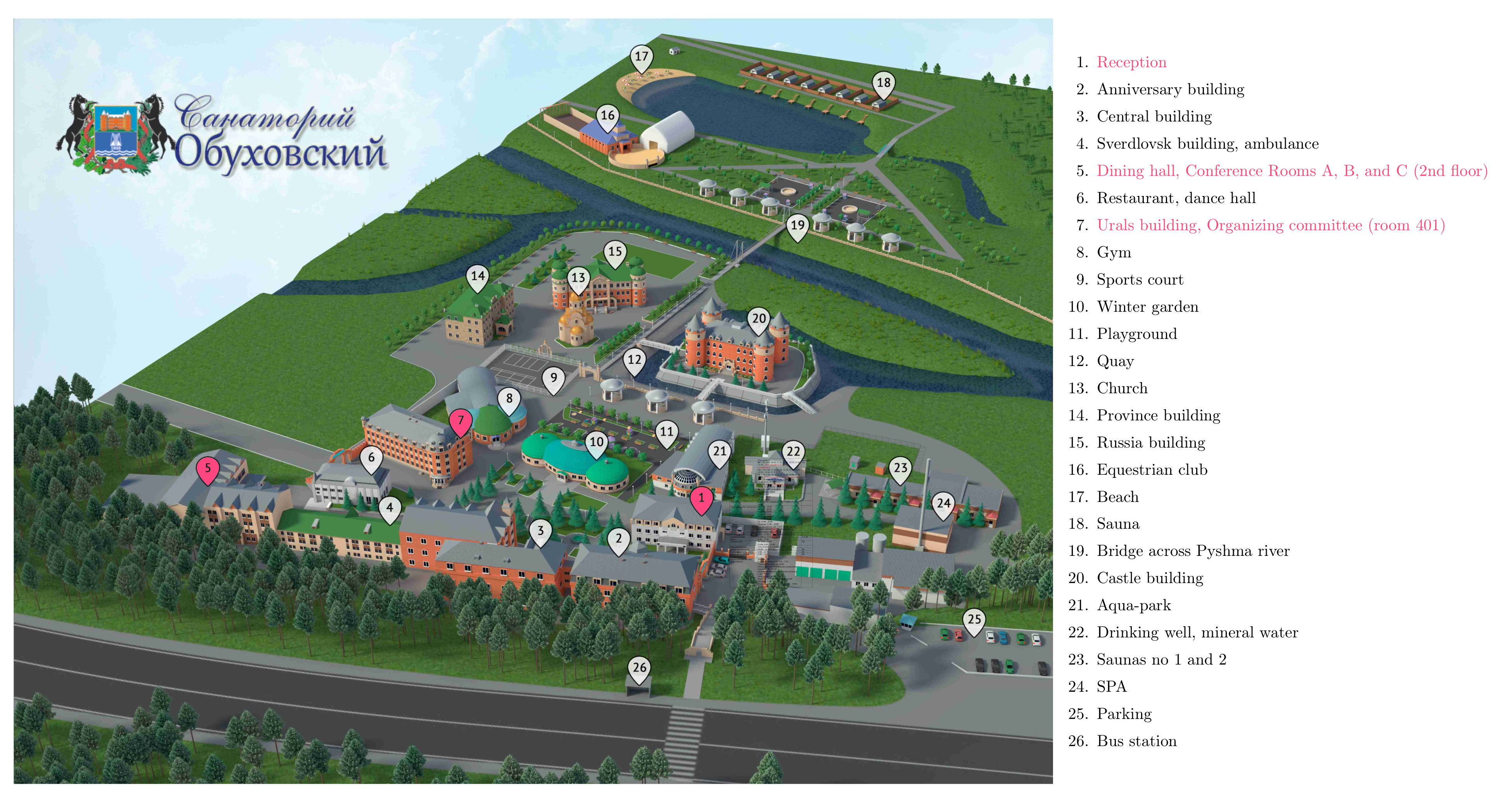
VENUE
room for 1 person
room
room for 1 person
room
- conference participants are invited to send a request to eni.obuhovski@mail.ru to issue the payment invoice for reservation.
- please, include to your request the following information: first name, last name, check-in date and time you prefer, check-out date and time, type of room (single or twin), contact phone number and e-mail to send the payment invoice;
- the e-mail response to the request will contain the payment invoice and billing information;
- each participant should pay the invoice and send a scanned copy of the receipt by e-mail at motor2019.registr@gmail.com;
- please keep your payment documents upon your arrival to the resort;
- All necessary payment confirmation documents can be issued upon request (an agreement, a participant certificate, acceptance certificate, receipt etc).